|
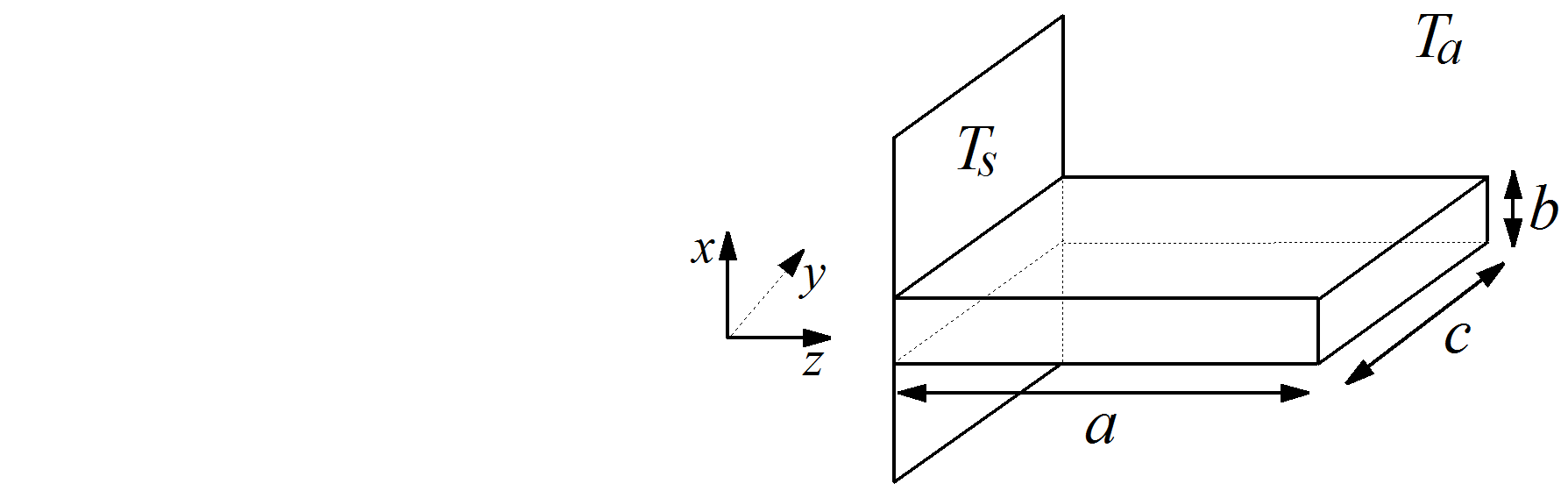
Tranferência de Calor em uma Aleta Retangular:Considere uma aleta retangular com dimensões \(a\) (na direção do eixo \(z\)), \(b\) (na direção do eixo \(y\)) e \(c\) (na direção do eixo \(x\)), conforme a figura a seguir ( Souza-Santos, 2007 ). Em linhas gerais, com a aleta objetiva-se aumentar a área de transferência de calor entre a superfície e o fluido circundante. A aleta retangular apresentada nesta figura é soldada a uma parede vertical que está a temperatura \(T_s\) em \(z\)=0 e a temperatura ambiente \(T_a\) em \(z\)=\(a\). Conforme destacado anteriormente, o objetivo é encontrar o perfil de temperatura na aleta considerando uma abordagem numérica, bem como comparar os resultados obtidos com os resultados analíticos. Hipóteses:Para a modelagem do sistema em análise são consideradas as seguintes hipóteses: \(i\)) estado estacionário, \(ii\)) na aleta, o calor é transferido por condução apenas na direção de \(z\) (neste caso, considera-se que as outras dimensões (\(x\) e \(y\)) são menos espessas do que a direção em \(z\)), \(iii\)) a condutividade térmica do material (\(\lambda\)) da aleta é constante, \(iv\)) o coeficiente de transferência de calor por convecção (\(\alpha\)) é constante, \(v\)) não existe mudança de fase. Modelagem Matemática:Baseando-se nestas hipóteses, o balanço de energia considera dois tipos de contribuição de calor, a saber, condução na direação de \(z\) e conveção (calor trocado entre a aleta e o ambiente). Matematicamente, o modelo que representa o fenômeno descrito é dado pela seguinte equação: \[\begin{gathered}
\label{Eq01}
\frac{d^2T}{dz^2}=\Phi(T-T_a)\\
\label{Eq01a}
T(z=0)=T_s\\
\label{Eq01b}
\frac{dT}{dz}(z=a)=0\end{gathered}\] em que \(z\) é a coordenada espacial e \(T\) é a temperatura. Conforme observado na figura acima, em \(z=\)0 a temperatura é igual a temperatura da parede (\(T_s\)) e em \(z=a\) considera-se que o fluxo de calor na direção de \(z\) é nulo, isto é, não existe fluxo de calor nesta direção.
\[\begin{gathered} \Phi=\frac{2\alpha(c+b)}{bc\lambda}\end{gathered}\] Solução Analítica:O modelo descrito tem solução analítica, dado por (para \(a\)=1): \[\begin{gathered}
\label{Eq02}
T(z)=-\frac{\exp(\sqrt{\Phi} z)\exp(-\sqrt{\Phi})}{\exp(-\sqrt{\Phi})+\exp(\sqrt{\Phi})}(T_a-T_s)-
\frac{\exp(-\sqrt{\Phi} z)\exp(\sqrt{\Phi})}{\exp(-\sqrt{\Phi})+\exp(\sqrt{\Phi})}(T_a-T_s)+T_a\end{gathered}\]
Solução Numérica:Para a simulação deste estudo de caso considera-se a aproximação de derivada segunda central para representar a derivada segunda presente na modelo diferencial, isto é: \[\begin{gathered} \label{Eq04} \frac{d^2T}{dz^2}\approx \frac{T_{i+1}-2T_{i}+T_{i-1}}{\Delta z^2},\;\;\;i=1, ..., n\end{gathered}\] em que \(T_{i+1}\), \(T_{i}\) e \(T_{i-1}\) representam as temperaturas nos pontos \(i+1\), \(i\) e \(i-1\), respectivamente, \(n\) é o número de pontos de discretização, \(\Delta z\) é o tamanho do passo de integração na direção de \(z\). Neste contexto, substituindo a aproximação descrita acima na equação diferencial original obtem-se o seguinte modelo discretizado: \[\begin{gathered} \label{Eq05} \frac{T_{i+1}-2T_{i}+T_{i-1}}{\Delta z^2}=\Phi(T_i-T_a),\;\;\;i=1, ..., n\end{gathered}\] Em se tratando da primeira condição de contorno, como esta representa o valor da temperatura em \(z\)=0, isto é; no ponto discretizado \(i\)=1, tem-se: \[\begin{gathered} \label{Eq05a} T_{1}=T_s\end{gathered}\] Já para avaliar a derivada primeira em \(z=a\) (que corresponde ao \(n\)-ésimo ponto discretizado), emprega-se uma aproximação para derivada à ré: \[\begin{gathered} \label{Eq05b} \frac{dT}{dz}\approx \frac{T_{n}-T_{n-1}}{\Delta z}\end{gathered}\] Assim sendo, a condição de contorno para \(z\)=\(a\) é dada pela seguinte relação: \[\begin{gathered} \frac{T_{n}-T_{n-1}}{\Delta z}=0\end{gathered}\] O modelo discretizado acima é linear, isto é; o mesmo pode ser representado na forma \(AT=B\), isto é: \[\begin{gathered} \label{Eq06a} T_{1}=T_s,\;\;\;i=1 \\ \label{Eq06b} \frac{1}{\Delta z^2}T_{i-1}+\Bigg(-\frac{2}{\Delta z^2}-\Phi\Bigg)T_{i}+\frac{1}{\Delta z^2}T_{i+1}=-\Phi T_a,\;\;\;i=2,...,n-1 \\ \label{Eq06c} -T_{n-1}+T_{n}=0,\;\;\;i=n\end{gathered}\] Matricialmente, para os \(n\) primeiros pontos, a matriz \(A\) e o vetor \(B\) são descritos como: \[AT=B\nonumber\] \[\left[\begin{array}{cccccc} 1 & 0 & 0 & \ldots & 0 & 0 \\ \displaystyle \frac{1}{\Delta z^2} & \displaystyle -\frac{2}{\Delta z^2}-\Phi & \displaystyle \frac{1}{\Delta z^2} & \ldots & 0 & 0\\ 0 & \displaystyle \frac{1}{\Delta z^2} & \displaystyle -\frac{2}{\Delta z^2}-\Phi & \ldots & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots& \vdots\\ 0 & 0 & 0 & \vdots & -1 & 1\\ \end{array}\right]\left[\begin{array}{c} T_1\\ T_2\\ T_3\\ \vdots \\ T_{n-1}\\ T_{n}\\ \end{array}\right]=\left[\begin{array}{c} T_s \\ -\displaystyle \Phi T_a \\ -\displaystyle \Phi T_a \\ \vdots \\ -\displaystyle \Phi T_a \\ 0 \end{array}\right]\] Conhecendo-se a matriz \(A\) e o vetor \(B\), o valor do vetor \(T\) pode ser obtido a partir da resolução do sistema \(AT=B\). Como este sistema apresenta um característica muito particular, isto é; o mesmo é tridiagonal, pode-se empregar o Algoritmo de Thomas. Simular o Perfil de Temperatura Análise de Sensibilidade Voltar para a página principal do LabSim-EQ |