|
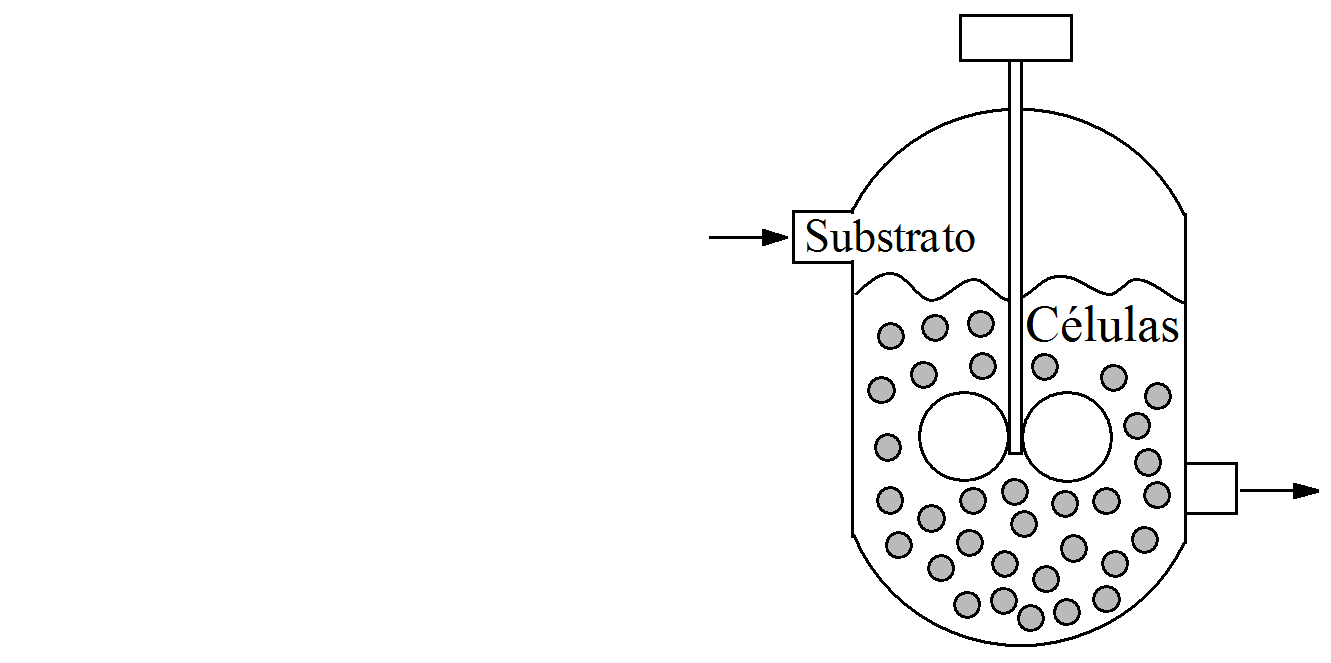
Reator Biológico:Considere um reator biológico em que as células se alimentam de uma corrente de substrato para secretar um produto de interesse. O objetivo deste estudo é analisar a condição de estado estacionário e os perfis dinâmicos das concentrações de células e substrato. Além disso, a estabilidade para cada estado estacionário é avaliada via determinaçãos dos autovalores da matriz Jacobiana do sistema diferencial considerado. Também é possível obter o plano de fases para esse sistema, de modo a analisar a dinâmica do modelo em termos do(s) estado(s) estacionário(s) obtido(s). Hipóteses:Para a modelagem desse sistema são consideradas as seguintes hipóteses (Bequette, 1998): \(i\)) propriedades físicas constantes; \(ii\)) o volume do reator é considerado constante; \(iii\)) processo isotérmico; \(iv\)) mistura perfeita; \(v\)) as vazões (volumétricas) do reação são consideradas constantes. Modelagem Matemática:Matematicamente, os perfis de concentração de células (\(x_1\)) e de substrato (\(x_2\)) em função do tempo (\(t\)) são descritos pelos seguintes balanços de massa: \[\frac{dx_1}{dt}=(\mu-D)x_1,\;\;x_1(0)=x_{1\circ}\] \[\frac{dx_2}{dt}=(s_f-x_2)D-\frac{\mu x_1}{Y},\;\;x_2(0)=x_{2\circ}\] em que \(\mu\) é a taxa específica de crescimento (ou cinética de crescimento), \(D\) é a taxa de diluição, \(s_f\) é a concentração de substrato na corrente de alimentação e \(Y\) é o rendimento do processo. \(x_{1\circ}\) e \(x_{2\circ}\) são as concentrações iniciais de células e substrato, respectivamente. Nesta aplicação considera-se uma expressão para \(\mu\) que apresenta inibição por substrato, isto é: \[\mu=\frac{\mu_{max}x_2}{k_m+x_2+k_1x_2^{2}}\] em que \(\mu_{max}\) é a taxa específica máxima de crescimento celular, \(k_m\) é a constante de saturação para o crescimento celular e \(k_1\) é um parâmetro que está relacionado com a inibição do crescimento celular pelo substrato. É importante ressaltar que se o parâmetro \(k_1\) for igual a zero, a expressão acima é conhecida como Modelo de Monod. Estado Estacionário:A condição de estado estacoinário é caracterizada pela não variação do vetor de variáveis dependentes com relação ao tempo. Assim, o modelo estacionário é calculado considerando que as derivadas de \(x_1\) e \(x_2\), com relação ao tempo, são iguais a zero, isto é: \[0=(\mu-D)x_1\] \[0=(s_f-x_2)D-\frac{\mu x_1}{Y}\] Apesar da não-linearidade inerente a este modelo, o mesmo apresenta solução analítica cujo número de soluções é função do valor do parâmetro \(k_1\). Se este parâmetro for igual a zero, tem-se o Modelo de Monod e o processo terá duas soluções (dois estados estacionários), dadas como:
\(\checkmark\) Primeiro Estado Estacionário:\[\begin{gathered} x_{1ee}=0\\ x_{2ee}=s_f\end{gathered}\] \(\checkmark\) Segundo Estado Estacionário:\[\begin{gathered} x_{1ee}={\frac {Y \left( -{\it s_f}\,{\it \mu_{max} }+{\it D}\,{\it s_f}+{\it D}\,{\it k_m} \right) }{-{\it \mu_{max} }+{\it D}}}\\ x_{2ee}=-{\frac {{\it D}\,{\it k_m}}{-{\it \mu_{max} }+{\it D}}} \end{gathered}\] em que \(x_{1ee}\) e \(x_{2ee}\) representam o estado estacionário para as concentrações de células e substrato, respectivamente. Para este último conjunto solução ressalta-se que, se os parâmetros \(\mu_{max}\) e \(D\) forem iguais, esse estado estacionário não poderá ser avaliado numericamente e apenas o primeiro estado estacionário será apresentado. Por outro lado, se este parâmetro for diferente de zero, tem-se o Modelo de Inibição por Substrato e o processo terá, a priori, três soluções (três estados estacionários), descritos como: \(\checkmark\)Primeiro Estado Estacionário:\[\begin{gathered} x_{1ee}=0\\ x_{2ee}=s_f\end{gathered}\] \(\checkmark\) Segundo Estado Estacionário:\[\begin{gathered} x_{1ee}=\frac{YD(s_f-x_{2ee})}{\mu(x_{2ee})}\\ x_{2ee}=-{\frac {-1/2\,{\it \mu_{max} }+1/2\,{\it D}-1/2\,\sqrt {{{\it \mu_{max} }} ^{2}-2\,{\it \mu_{max} }\,{\it D}+{{\it D}}^{2}-4\,{{\it D}}^{2}{\it k_1}\,{\it k_m}}}{{\it D}\,{\it k_1}}}\\ \mu(x_{2ee})=\frac{\mu_{max}x_{2ee} }{k_m+x_{2ee}+k_1x_{2ee}^{2}} \end{gathered}\] \(\checkmark\) Terceiro Estado Estacionário:\[\begin{gathered} x_{1ee}=\frac{YD(s_f-x_{2ee})}{\mu(x_{2ee})}\\ x_{2ee}=-{\frac {-1/2\,{\it \mu_{max} }+1/2\,{\it D}+1/2\,\sqrt {{{\it \mu_{max} }} ^{2}-2\,{\it \mu_{max} }\,{\it D}+{{\it D}}^{2}-4\,{{\it D}}^{2}{\it k_1}\,{\it k_m}}}{{\it D}\,{\it k_1}}}\\ \mu(x_{2ee})=\frac{\mu_{max}x_{2ee} }{k_m+x_{2ee}+k_1x_{2ee}^{2}} \end{gathered}\] É importante enfatizar que se o termo contido dentro da raiz quadrada destes últimos dois pontos estacionários for menor do que zero, somente uma solução fisicamente viável (no campo dos reais) será obtida. Neste caso, sempre serão apresentados os resultados de estado estacionário para soluções fisicamente viáveis, sendo uma mensagem apresentada para o usuário. Assim, pode-se avaliar a vialbilidade das magnitudes dos parâmetros definidos pelo usuário. Solução Numérica:O sistema que representa a variação das concentrações em função do tempo é diferencial de primeira ordem. Neste caso, o mesmo pode ser integrado numericamente usando diferentes abordagens. Nesta aplicação será empregado o Algoritmo de Runge Kutta 4a Ordem a partir das condições iniciais e número de pontos de discretização definidos pelo usuário. Análise de Estabilidade:Para analisar a estabilidade de um sistema não linear, os autovalores da matriz Jacobiana referente ao modelo considerado devem ser determinados. Esta análise deve ser realizada para cada ponto estacionário encontrado. Na prática, pode-se ter um estado estacionário fisicamente viável, mas o mesmo pode ser instável, isto é; o sistema dinâmico quanto o tempo tender a infinito não tenderá para o mesmo (exceto se este ponto seja considerado como condição inicial para o sistema - neste caso, o sistema já estará em regime estacionário logo de início e só sairá desta condição se um ou mais parâmetros do modelo sejam modificados). Os autovalores (\(\lambda\)) são as raízes do polinômio característico obtido de acordo com a seguinte expressão: \[\begin{gathered} \det(J-\lambda I)=0 \end{gathered}\] em que \(J\) é a matriz Jacobiana avaliada no ponto estacionário em análise e \(I\) é matriz identidade (de mesma dimensão com relação à Jacobiana). Para o modelo do reator biológico, a matriz Jacobina considerando inibição por substrato para um estado estacionário genérico (\(x_{1ee}\) e \(x_{2ee}\)) é dado como segue: \[J= \left[ \begin {array}{cc} {\displaystyle \frac {{\it \mu_{max}}\,{\it x_{2ee} }}{{\it k_m}+{\it x_{2ee} }+{\it k_1}\,{{\it x_{2ee} }}^{2}}}-{\it D}& \left( {\displaystyle \frac {{\it \mu_{max}}}{{\it k_m}+{\it x_{2ee} }+{\it k_1}\,{{\it x_{2ee} }}^{2}}}-{\displaystyle \frac {{\it \mu_{max}}\,{\it x_{2ee} }\, \left( 1+2\,{\it k_1}\,{\it x_{2ee} } \right) }{ \left( {\it k_m}+{\it x_{2ee} }+{\it k_1}\,{{\it x_{2ee} }}^{2} \right) ^{2}}} \right) { \it x_{1ee} }\\ -{\displaystyle \frac {{\it \mu_{max}}\,{\it x_{2ee} }}{ \left( {\it k_m}+{\it x_{2ee} }+{\it k_1}\,{{\it x_{2ee} }}^{2} \right) Y}}&-{\it D}-{ \displaystyle \frac {{\it \mu_{max}}\,{\it x_{1ee} }}{ \left( {\it k_m}+{\it x_{2ee} }+{\it k_1}\,{{ \it x_{2ee} }}^{2} \right) Y}}+{\displaystyle \frac {{\it \mu_{max}}\,{\it x_{2ee} }\,{\it x_{1ee} }\, \left( 1+2\,{\it k_1}\,{\it x_{2ee} } \right) }{ \left( {\it k_m}+{\it x_{2ee} }+{ \it k_1}\,{{\it x_{2ee} }}^{2} \right) ^{2}Y}}\end {array} \right]\] Ao se avaliar esta matriz para um estado estacionário genérico obtêm-se os seguintes autovalores para o problema de interesse. \[\begin{gathered} \lambda_1=-{\it D} \end{gathered}\] \[\begin{gathered} \lambda_2=-{\frac {\phi_1+\phi_2+\phi_3}{\phi_4 }}\\ \end{gathered}\] onde: \[\begin{gathered} \phi_1={\it D}\,Y{{\it k_1}}^{2}{{\it x_{2ee} }}^{4}+2\,{\it D}\,Y{\it k_m }\,{\it k_1}\,{{\it x_{2ee}}}^{2}-{\it \mu_{max} }\,{\it x_{1ee} }\,{\it k_1}\,{{\it x_{2ee} }}^{2}+2\,{\it D}\,Y{\it k_1}\,{{\it x_{2ee} }}^{3}\\ \phi_2=-Y{\it \mu_{max} }\,{{\it x_{2ee} }}^{3}{\it k_1}-Y{\it \mu_{max} }\,{{\it x_{2ee} }}^{2}+{\it D}\,Y{{\it x_{2ee} }}^ {2}-Y{\it \mu_{max} }\,{\it x_{2ee} k_m}\, \\ \phi_3=2\,{\it D}\,Y{\it k_m}\,{\it x_{2ee}}+{\it D}\,Y{{\it k_m}}^{2}+{\it \mu_{max} }\,{\it x_{1ee} }\,{\it k_m}\\ \phi_4=Y \left( {{\it k_m}}^{2}+2\,{\it k_m}\,{\it x_{2ee} }+2\,{\it k_m}\,{\it k_1}\,{{ \it x_{2ee} }}^{2}+{{\it x_{2ee} }}^{2}+2\,{\it k_1}\,{{\it x_{2ee} }}^{3}+{{\it k_1}}^{2} {{\it x_{2ee} }}^{4} \right) \end{gathered}\] Para o caso do Modelo de Monod, basta fazer \(k_1\) igual a zero nas equações acima. Plano de Fase:O plano de fase (ou retrato de fase) corresponde a uma exibição visual onde deseja-se avaliar a convergência do modelo para o estado estacionário estável. Para esta finalidade, os resultados obtidos com a simulação dos modelos dinamicamente são plotados não em função da variável temporal, mas sim em termos do vetor de variáveis dependentes. No caso do problema do reator biológico, plota-se os perfis das concentrações de células e de substrato um contra o outro para diferentes condições iniciais. Se nesta mesma figura também for plotado todos os estados estacionários encontrados. pode-se avaliar a convergência do processo em termos da condição inicial utilizada. Por exemplo, se para um dado conjunto de parâmetros o processo tiver dois estados estacionários estáveis, a depender da condição inicial utilizada, pode-se caminhar para um ou outro estado estacionário. Se também for plotado neste mesmo gráfico um ponto estacionário instável, pode-se verificar que o processo nunca alcançara o mesmo, a não ser que a condição inicial seja o próprio ponto estacionário, conforme descrito anteriormente. Em termos de implementação, o plano de fases para o reator biológico será plotado considerando 40 condições iniciais diferentes e definidas de acordo com os limites mínimos e máximos observados para as soluções obtidas com um determinado conjunto de parâmetros. Este número de combinações foi escolhido de forma a não prejudicar a visualização dos resultados. Neste caso, o usuário apenas terá que definir todos os parâmetros de entrada do modelo, exceto as condições iniciais. A solução do estado estacionário para um dado conjunto de parâmetros definidos é calculado e os limites para o plano de fase são calculados automaticamente. Por fim é apresentado o plano de fases para o problema em análise. Simular os Perfis de Concentração Análise de Sensibilidade Plano de Fase Voltar para a página principal do LabSim-EQ |